22.03.01 - Search Space and Search Tree
Problem Search Space
Define the problem as a search. Important in science and engineering. Any problem can be seen as a search for the 'right answer'
Search Space - Set of all possible solutions to a problem Search Algorithms - Input: a problem, Return: a solution to the problem
Trees
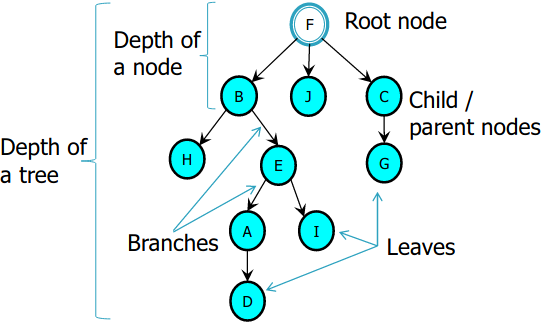 Shows how the data can be represented
Shows how the data can be represented
Trees vs. Search Space
States - nodes | Possible states of the problem Search Space - all nodes in the tree | Set of all states reachable from the initial state Operator - branches | Set of actions that move one state to another
Neighbourhood - All possible states reachable from a given state Goal Test - Test to a state tell if the search reached a state that solves the problem Path cost - How much it costs to take a particular path
By using states and operators we can define the problem into the nodes and branches in a search tree. If you check all of the possible states, the possible states should be included in the tree.
Improve Search Techniques:
- Define the problem into smaller search tree
- Improve search efficiency through the tree
Search Trees
Issues
Tree Size: Branching Factor: Average no. of branches of all nodes in a tree.
Claude Shannon (1949): how computers could play chess
Search trees grow very quickly (exponentially)
General Search
Function General-Search(p, QUEUING-FN) returns a solution or failure
nodes = Make-Queue(Make-Node(Initial-State[p]))
Loop do
If nodes is empty then return failure
node = Remove-Front(nodes)
If Goal-Test[p] on State(node) succeeds then returm node
nodes = QUEUING-FN(nodes, Expand(node, Operators[p]))
End
End Function
Data structures: nodes:Queue; nodes:state;